Salam...
Blog nie aku buat khas untuk memenuhi kehendak lecturer aku..EN ZAKI MASUD BAGI subject NETWORK SECURITY.
Sunday, July 19, 2009
SeCuRiTy LiFe
Posted by SeCuRiTy LiFe.. at 11:05 PM
Subscribe to:
Post Comments (Atom)
Blog nie DIbuat khas bagi memenuhi syarat subject Information Technologies Security (BITS 3413).
Salam...
Blog nie aku buat khas untuk memenuhi kehendak lecturer aku..EN ZAKI MASUD BAGI subject NETWORK SECURITY.
Posted by SeCuRiTy LiFe.. at 11:05 PM
Apakah pendirian hidupmu?

Azamku tak mungkin kau jadikan kelabu Tepis-tepis kata yg sinis Yang panas ku jadikan membeku Bahagia aku kemudi selalu Biar ku menuju jalan tak berbiku Biarkan cemburu berkubur Asalkan tak cemari hidupku Biarkan ku senyum selalu Tandanya ku tiada seteru Jangan kau terpenjuru Jangan kau bercelaru Diriku bukan milikmu*
"Ya Allah... Tunjukkan kepada kami yang benar dan jadikan pilihan kami mengikuti yang benar itu. Dan juga tunjukkan kepada kami yang tidak benar dan permudahkan kami meninggalkannya."
|
|
Make your own Countdown Clocks![]()
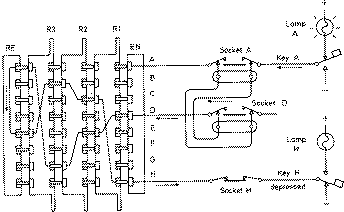
Network security starts from authenticating the user, commonly with a username and a password. Since this requires just one thing besides the user name, i.e. the password which is something you 'know', this is sometimes termed one factor authentication. With two factor authentication something you 'have' is also used (e.g. a security token or 'dongle', an ATM card, or your mobile phone), or with three factor authentication something you 'are' is also used (e.g. a fingerprint or retinal scan).
Once authenticated, a firewall enforces access policies such as what services are allowed to be accessed by the network users .Though effective to prevent unauthorized access, this component may fail to check potentially harmful content such as computer worms or Trojans being transmitted over the network. Anti-virus software or an intrusion prevention system (IPS)[2] help detect and inhibit the action of such malware. An anomaly-based intrusion detection system may also monitor the network and traffic for unexpected (i.e. suspicious) content or behaviour and other anomalies to protect resources, e.g. from denial of service attacks or an employee accessing files at strange times. Individual events occurring on the network may be logged for audit purposes and for later high level analysis.
Communication between two hosts using the network could be encrypted to maintain privacy.
Honeypots, essentially decoy network-accessible resources, could be deployed in a network as surveillance and early-warning tools. Techniques used by the attackers that attempt to compromise these decoy resources are studied during and after an attack to keep an eye on new exploitation techniques. Such analysis could be used to further tighten security of the actual network being protected by the honeypot.
A useful summary of standard concepts and methods in network security is given by in the form of an extensible ontology of network security attacks.
IPSec is a framework of open standards developed by the Internet Engineering Task Force (IETF). IPSec provides security for transmission of sensitive information over unprotected networks such as the Internet. IPSec acts at the network layer, protecting and authenticating IP packets between participating IPSec devices ("peers"), such as Cisco routers. IPSec provides the following network security services. These services are optional. In general, local security policy will dictate the use of one or more of these services: • • • • IPSec Network Security
Description
![]() Data Confidentiality—The IPSec sender can encrypt packets before transmitting them across a network.
Data Confidentiality—The IPSec sender can encrypt packets before transmitting them across a network. ![]() Data Integrity—The IPSec receiver can authenticate packets sent by the IPSec sender to ensure that the data has not been altered during transmission.
Data Integrity—The IPSec receiver can authenticate packets sent by the IPSec sender to ensure that the data has not been altered during transmission. ![]() Data Origin Authentication—The IPSec receiver can authenticate the source of the IPSec packets sent. This service is dependent upon the data integrity service.
Data Origin Authentication—The IPSec receiver can authenticate the source of the IPSec packets sent. This service is dependent upon the data integrity service. ![]() Anti-Replay—The IPSec receiver can detect and reject replayed packets.
Anti-Replay—The IPSec receiver can detect and reject replayed packets.


The RSA algorithm involves three steps: key generation, encryption and decryption.
RSA involves a public key and a private key. The public key can be known to everyone and is used for encrypting messages. Messages encrypted with the public key can only be decrypted using the private key. The keys for the RSA algorithm are generated the following way:
 .
. e and
e and  share no divisors other than 1 (i.e. e and
share no divisors other than 1 (i.e. e and  are coprime).
are coprime).  .
. The public key consists of the modulus n and the public (or encryption) exponent e. The private key consists of the modulus n and the private (or decryption) exponent d which must be kept secret.
Notes on some variants:
 , where lcm is the least common multiple instead of
, where lcm is the least common multiple instead of  .
. and
and  ,
, .
.Alice transmits her public key (n,e) to Bob and keeps the private key secret. Bob then wishes to send message M to Alice.
He first turns M into an integer 0 < m < n by using an agreed-upon reversible protocol known as a padding scheme. He then computes the ciphertext c corresponding to:

This can be done quickly using the method of exponentiation by squaring. Bob then transmits c to Alice.
Alice can recover m from c by using her private key exponent d by the following computation:

Given m, she can recover the original message M by reversing the padding scheme.
The above decryption procedure works because:
 .
.Now, since  ,
,
 .
.The last congruence directly follows from Euler's theorem when m is relatively prime to n. Using the Chinese remainder theorem, it can be shown that the equations holds for all m.
This shows that we get the original message back:

Here is an example of RSA encryption and decryption. The parameters used here are artificially small, but one can also use OpenSSL to generate and examine a real keypair.



 e.g., by computing the modular multiplicative inverse of e modulo
e.g., by computing the modular multiplicative inverse of e modulo  :
:
The public key is (n = 3233, e = 17). For a padded message m the encryption function is:

The private key is (n = 3233, d = 2753). The decryption function is:

For example, to encrypt m = 123, we calculate

To decrypt c = 855, we calculate
 .
.Both of these calculations can be computed efficiently using the square-and-multiply algorithm for modular exponentiation. In real life situations the primes selected would be much larger, however in our example it would be relatively trivial to factor n, 3233, obtained from the freely available public key back to the primes p and q. Given e, also from the public key, we could then compute d and so acquire the private key.
When used in practice, RSA is generally combined with some padding scheme. The goal of the padding scheme is to prevent a number of attacks that potentially work against RSA without padding:
 Because of this multiplicative property a chosen-ciphertext attack is possible. E.g. an attacker, who wants to know the decryption of a ciphertext c = memod n may ask the holder of the private key to decrypt an unsuspicious-looking ciphertext c' = cremod n for some value r chosen by the attacker. Because of the multiplicative property c' is the encryption of mrmod n. Hence, if the attacker is successful with the attack, he will learn mrmod n from which he can derive the message m by multiplying mr with the modular inverse of r modulo n.
Because of this multiplicative property a chosen-ciphertext attack is possible. E.g. an attacker, who wants to know the decryption of a ciphertext c = memod n may ask the holder of the private key to decrypt an unsuspicious-looking ciphertext c' = cremod n for some value r chosen by the attacker. Because of the multiplicative property c' is the encryption of mrmod n. Hence, if the attacker is successful with the attack, he will learn mrmod n from which he can derive the message m by multiplying mr with the modular inverse of r modulo n.To avoid these problems, practical RSA implementations typically embed some form of structured, randomized padding into the value m before encrypting it. This padding ensures that m does not fall into the range of insecure plaintexts, and that a given message, once padded, will encrypt to one of a large number of different possible ciphertexts.
Standards such as PKCS#1 have been carefully designed to securely pad messages prior to RSA encryption. Because these schemes pad the plaintext m with some number of additional bits, the size of the un-padded message M must be somewhat smaller. RSA padding schemes must be carefully designed so as to prevent sophisticated attacks which may be facilitated by a predictable message structure. Early versions of the PKCS#1 standard (up to version 1.5) used a construction that turned RSA into a semantically secure encryption scheme. This version was later found vulnerable to a practical adaptive chosen ciphertext attack. Later versions of the standard include Optimal Asymmetric Encryption Padding (OAEP), which prevents these attacks. The PKCS#1 standard also incorporates processing schemes designed to provide additional security for RSA signatures, e.g, the Probabilistic Signature Scheme for RSA (RSA-PSS).
Suppose Alice uses Bob's public key to send him an encrypted message. In the message, she can claim to be Alice but Bob has no way of verifying that the message was actually from Alice since anyone can use Bob's public key to send him encrypted messages. So, in order to verify the origin of a message, RSA can also be used to sign a message.
Suppose Alice wishes to send a signed message to Bob. She can use her own private key to do so. She produces a hash value of the message, raises it to the power of dmod n (as she does when decrypting a message), and attaches it as a "signature" to the message. When Bob receives the signed message, he uses the same hash algorithm in conjunction with Alice's public key. He raises the signature to the power of emod n (as he does when encrypting a message), and compares the resulting hash value with the message's actual hash value. If the two agree, he knows that the author of the message was in possession of Alice's private key, and that the message has not been tampered with since.
Note that secure padding schemes such as RSA-PSS are as essential for the security of message signing as they are for message encryption, and that the same key should never be used for both encryption and signing purposes.
The security of the RSA cryptosystem is based on two mathematical problems: the problem of factoring large numbers and the RSA problem. Full decryption of an RSA ciphertext is thought to be infeasible on the assumption that both of these problems are hard, i.e., no efficient algorithm exists for solving them. Providing security against partial decryption may require the addition of a secure padding scheme.[citation needed]
The RSA problem is defined as the task of taking eth roots modulo a composite n: recovering a value m such that c = memod n, where (n,e) is an RSA public key and c is an RSA ciphertext. Currently the most promising approach to solving the RSA problem is to factor the modulus n. With the ability to recover prime factors, an attacker can compute the secret exponent d from a public key (n,e), then decrypt c using the standard procedure. To accomplish this, an attacker factors n into p and q, and computes (p − 1)(q − 1) which allows the determination of d from e. No polynomial-time method for factoring large integers on a classical computer has yet been found, but it has not been proven that none exists. See integer factorization for a discussion of this problem.
As of 2008[update], the largest (known) number factored by a general-purpose factoring algorithm was 663 bits long (see RSA-200), using a state-of-the-art distributed implementation. The next record is probably going to be a 768 bits modulus[5]. RSA keys are typically 1024–2048 bits long. Some experts believe that 1024-bit keys may become breakable in the near term (though this is disputed); few see any way that 4096-bit keys could be broken in the foreseeable future. Therefore, it is generally presumed that RSA is secure if n is sufficiently large. If n is 300 bits or shorter, it can be factored in a few hours on a personal computer, using software already freely available. Keys of 512 bits have been shown to be practically breakable in 1999 when RSA-155 was factored by using several hundred computers and are now factored in a few weeks using common hardware.[6] A theoretical hardware device named TWIRL and described by Shamir and Tromer in 2003 called into question the security of 1024 bit keys. It is currently recommended that n be at least 2048 bits long.[7]
In 1994, Peter Shor showed that a quantum computer could factor in polynomial time, breaking RSA. However, only small scale quantum computers have been realized.[citation needed]
Finding the large primes p and q is usually done by testing random numbers of the right size with probabilistic primality tests which quickly eliminate virtually all non-primes.
Numbers p and q should not be 'too close', lest the Fermat factorization for n be successful, if p − q, for instance is less than 2n1 / 4 (which for even small 1024-bit values of n is 3×1077) solving for p and q is trivial. Furthermore, if either p − 1 or q − 1 has only small prime factors, n can be factored quickly by Pollard's p − 1 algorithm, and these values of p or q should therefore be discarded as well.
It is important that the private key d be large enough. Michael J. Wiener showed[8] that if p is between q and 2q (which is quite typical) and d < n1 / 4 / 3, then d can be computed efficiently from n and e. There is no known attack against small public exponents such as e = 3, provided that proper padding is used. However, when no padding is used or when the padding is improperly implemented then small public exponents have a greater risk of leading to an attack, such as for example the unpadded plaintext vulnerability listed above. 65537 is a commonly used value for e. This value can be regarded as a compromise between avoiding potential small exponent attacks and still allowing efficient encryptions (or signature verification). The NIST Special Publication on Computer Security (SP 800-78 Rev 1 of August 2007) does not allow public exponents e smaller than 65537, but does not state a reason for this restriction.
RSA is much slower than DES and other symmetric cryptosystems. In practice, Bob typically encrypts a secret message with a symmetric algorithm, encrypts the (comparatively short) symmetric key with RSA, and transmits both the RSA-encrypted symmetric key and the symmetrically-encrypted message to Alice.
This procedure raises additional security issues. For instance, it is of utmost importance to use a strong random number generator for the symmetric key, because otherwise Eve (an eavesdropper wanting to see what was sent) could bypass RSA by guessing the symmetric key.
As with all ciphers, how RSA public keys are distributed is important to security. Key distribution must be secured against a man-in-the-middle attack. Suppose Eve has some way to give Bob arbitrary keys and make him believe they belong to Alice. Suppose further that Eve can intercept transmissions between Alice and Bob. Eve sends Bob her own public key, which Bob believes to be Alice's. Eve can then intercept any ciphertext sent by Bob, decrypt it with her own private key, keep a copy of the message, encrypt the message with Alice's public key, and send the new ciphertext to Alice. In principle, neither Alice nor Bob would be able to detect Eve's presence. Defenses against such attacks are often based on digital certificates or other components of a public key infrastructure.
Kocher described a new attack on RSA in 1995: if the attacker Eve knows Alice's hardware in sufficient detail and is able to measure the decryption times for several known ciphertexts, she can deduce the decryption key d quickly. This attack can also be applied against the RSA signature scheme. In 2003, Boneh and Brumley demonstrated a more practical attack capable of recovering RSA factorizations over a network connection (e.g., from a Secure Socket Layer (SSL)-enabled webserver). This attack takes advantage of information leaked by the Chinese remainder theorem optimization used by many RSA implementations.
One way to thwart these attacks is to ensure that the decryption operation takes a constant amount of time for every ciphertext. However, this approach can significantly reduce performance. Instead, most RSA implementations use an alternate technique known as cryptographic blinding. RSA blinding makes use of the multiplicative property of RSA. Instead of computing cdmod n, Alice first chooses a secret random value r and computes (rec)dmod n. The result of this computation is  and so the effect of r can be removed by multiplying by its inverse. A new value of r is chosen for each ciphertext. With blinding applied, the decryption time is no longer correlated to the value of the input ciphertext and so the timing attack fails.
and so the effect of r can be removed by multiplying by its inverse. A new value of r is chosen for each ciphertext. With blinding applied, the decryption time is no longer correlated to the value of the input ciphertext and so the timing attack fails.
In 1998, Daniel Bleichenbacher described the first practical adaptive chosen ciphertext attack, against RSA-encrypted messages using the PKCS #1 v1 padding scheme (a padding scheme randomizes and adds structure to an RSA-encrypted message, so it is possible to determine whether a decrypted message is valid.) Due to flaws with the PKCS #1 scheme, Bleichenbacher was able to mount a practical attack against RSA implementations of the Secure Socket Layer protocol, and to recover session keys. As a result of this work, cryptographers now recommend the use of provably secure padding schemes such as Optimal Asymmetric Encryption Padding, and RSA Laboratories has released new versions of PKCS #1 that are not vulnerable to these attacks.
Branch prediction analysis is also called BPA. Many processors use a branch predictor to determine whether a conditional branch in the instruction flow of a program is likely to be taken or not. Usually these processors also implement simultaneous multithreading (SMT). Branch prediction analysis attacks use a spy process to discover (statistically) the private key when processed with these processors.
Simple Branch Prediction Analysis (SBPA) claims to improve BPA in a non-statistical way. In their paper, "On the Power of Simple Branch Prediction Analysis", the authors of SBPA (Onur Aciicmez and Cetin Kaya Koc) claim to have discovered 508 out of 512 bits of an RSA key in 10 iterations.
DES applies a 56-bit key to each 64-bit block of data. The process can run in several modes and involves 16 rounds or operations. Although this is considered "strong" encryption, many companies use "triple DES", which applies three keys in succession. This is not to say that a DES-encrypted message cannot be "broken." Early in 1997, Rivest-Shamir-Adleman, owners of another encryption approach, offered a $10,000 reward for breaking a DES message. A cooperative effort on the Internet of over 14,000 computer users trying out various keys finally deciphered the message, discovering the key after running through only 18 quadrillion of the 72 quadrillion possible keys! Few messages sent today with DES encryption are likely to be subject to this kind of code-breaking effort.
DES originated at IBM in 1977 and was adopted by the U.S. Department of Defense. It is specified in the ANSI X3.92 and X3.106 standards and in the Federal FIPS 46 and 81 standards. Concerned that the encryption algorithm could be used by unfriendly governments, the U.S. government has prevented export of the encryption software. However, free versions of the software are widely available on bulletin board services and Web sites. Since there is some concern that the encryption algorithm will remain relatively unbreakable, NIST has indicated DES will not be recertified as a standard and submissions for its replacement are being accepted. The next standard will be known as the Advanced Encryption Standard (AES).

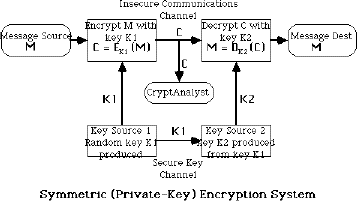
Encryption C = E_(K)(P)
Decryption P = E_(K)^(-1)(C)
E_(K) is chosen from a family of transformations known as a cryptographic system.
The parameter that selects the individual transformation is called the key K, selected from a keyspace K
More formally a cryptographic system is a single parameter family of invertible transformations
E_(K) ; K in K : P -> C
with the inverse algorithm E_(K)^(-1) ; K in K : C -> P
such that the inverse is unique
Usually assume the cryptographic system is public, and only the key is secret information
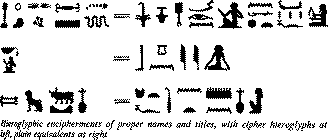

L FDPH L VDZ L FRQTXHUHG
I CAME I SAW I CONQUERED
 ie mapping is
ie mapping is ABCDEFGHIJKLMNOPQRSTUVWXYZ
DEFGHIJKLMNOPQRSTUVWXYZABC
Decryption D_(k) : i -> i - k mod 26
GDUCUGQFRMPCNJYACJCRRCPQ
HEVDVHRGSNQDOKZBDKDSSDQR
Plain - IFWEWISHTOREPLACELETTERS
JGXFXJTIUPSFQMBDFMFUUFST
KHYGYKUJVQTGRNCEGNGVVGTU
Cipher - LIZHZLVKWRUHSODFHOHWWHUV
MJAIAMWLXSVITPEGIPIXXIVW
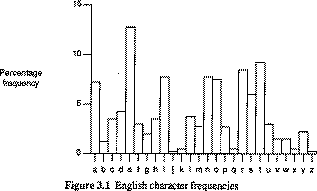
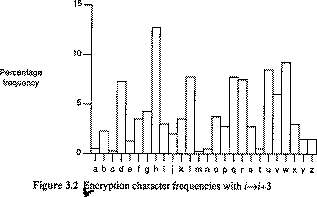
Single Letter Double Letter Triple Letter
E TH THE
T HE AND
R IN TIO
N ER ATI
I RE FOR
O ON THA
A AN TER
S EN RES
nb a must not divide 26 (ie gcd(a,26) = 1)
otherwise cipher is not reversible eg a=2
and a=0, b=1, c=2 ... , y=24, z=25
Example - Sinkov pp 34-35
Plain: ABCDEFGHIJKLMNOPQRSTUVWXYZ
Cipher: DKVQFIBJWPESCXHTMYAUOLRGZN
Plaintext: IFWEWISHTOREPLACELETTERS
Ciphertext: WIRFRWAJUHYFTSDVFSFUUFYA
2) can solve the problem piece by piece
(ie can get key nearly right, and nearly get message)
(near enough MUST NOT be good enough!)
Cryptanalysis
Example Seberry p66
STARW
BCDEF
GHIJK
LMNOP
QUVXY
Z
Plain: ABCDEFGHIJKLMNOPQRSTUVWXYZ
Cipher: SBGLQZTCHMUADINVREJOXWFKPY
Plaintext: I KNOW ONLY THAT I KNOW NOTHING
Ciphertext: H UINF NIAP OCSO H UINF INOCHIT
Plaintext THISPROCESSCANALSOBEEXPRESSED
Keyword CIPHERCIPHERCIPHERCIPHERCIPHE
Plaintext VPXZTIQKTZWTCVPSWFDMTETIGAHLH

ABCDEFGHIJKLMNOPQRSTUVWXYZ
A ABCDEFGHIJKLMNOPQRSTUVWXYZ
B BCDEFGHIJKLMNOPQRSTUVWXYZA
C CDEFGHIJKLMNOPQRSTUVWXYZAB
D DEFGHIJKLMNOPQRSTUVWXYZABC
E EFGHIJKLMNOPQRSTUVWXYZABCD
F FGHIJKLMNOPQRSTUVWXYZABCDE
G GHIJKLMNOPQRSTUVWXYZABCDEF
H HIJKLMNOPQRSTUVWXYZABCDEFG
I IJKLMNOPQRSTUVWXYZABCDEFGH
J JKLMNOPQRSTUVWXYZABCDEFGHI
K KLMNOPQRSTUVWXYZABCDEFGHIJ
L LMNOPQRSTUVWXYZABCDEFGHIJK
M MNOPQRSTUVWXYZABCDEFGHIJKL
N NOPQRSTUVWXYZABCDEFGHIJKLM
O OPQRSTUVWXYZABCDEFGHIJKLMN
P PQRSTUVWXYZABCDEFGHIJKLMNO
Q QRSTUVWXYZABCDEFGHIJKLMNOP
R RSTUVWXYZABCDEFGHIJKLMNOPQ
S STUVWXYZABCDEFGHIJKLMNOPQR
T TUVWXYZABCDEFGHIJKLMNOPQRS
U UVWXYZABCDEFGHIJKLMNOPQRST
V VWXYZABCDEFGHIJKLMNOPQRSTU
W WXYZABCDEFGHIJKLMNOPQRSTUV
X XYZABCDEFGHIJKLMNOPQRSTUVW
Y YZABCDEFGHIJKLMNOPQRSTUVWX
Z ZABCDEFGHIJKLMNOPQRSTUVWXY
then f_(i) (a) = a + k_(i) (mod n)
then f_(i) (a) = (k_(i) - a) (mod n)
and its inverse is
f_(i) ^(-1)(a) = (k_(i) - c) (mod n)
Example - Seberry p71
Key = d
Plain: ABCDEFGHIJKLMNOPQRSTUVWXYZ
Cipher: DCBAZYXWVUTSRQPONMLKJIHGFE
then f_(i) (a) = a - k_(i) (mod n)
where H(K) is entropy (amount of info) of the key,
and is D the rate of the language used (eg 3.2)
hence only need 2 letters to break
hence only need 27 or 28 letters to break
hence need 1.5 times the number of separate substitutions used letters to break the cipher
Example - Seberry p71
Plaintext: TOBEORNOTTOBE
Key: NOWNOWNOWNOWN
Ciphertext: GCXRCNACPGCXR
Since repeats are 9 chars apart, guess period is 3 or 9.
see Seberry Table 3.2 p72 and Table 3.3 p74
d IC
1 0.0660
2 0.0520
3 0.0473
4 0.0450
5 0.0436
6 0.0427
7 0.0420
8 0.0415
9 0.0411
10 0.0408
11 0.0405
12 0.0403
13 0.0402
14 0.0400
15 0.0399
... ...
Inf 0.0380
Table 3.3 - Period and IC for English
MR = Isu(i=o,n-1,(p_(i) - F(1,n))^(2))where p_(i) is probability an arbitrary character in ciphertext is the ith character a_(i) in the alphabet
Isu(i=o,n-1,p_(i)) = 1
MR = Isu(i=o,n-1,p_(i)^(2)) - 0.038or
MR + 0.038 = Isu(i=o,n-1,p_(i)^(2))is prob two arbitrary letters in ciphertext are the same
Bbc[(S(N,2)) = F(1,2) N (N-1)
F(F_(i)(F_(i)-1),2) and Isu(i=o,n-1,F_(i)) = 1
IC = Isu(i=o,n-1,F(F_(i)(F_(i)-1),N(N-1)))and use the IC estimate in
MR + 0.038 = IC
0.038 < IC < 0.066
Exp(IC) = F(1,d) F(N-d,N-1)(0.066) + Bbc[(S(d-1,d))F(N,N-1)(0.038)and we can use these values to estimate d from the ciphertext
Example program to compute IC - Seberry Fig3.4 p74
Example - Seberry pp73-77
Command Meaning
? this message.
! execute a shell command.
f [[n]] print [the n most] frequent strings of length seqlen.
g [] print the frequency distribution graph of letters.
i [] calculate the index of coincidence of the text.
l [ ] list only the modified string. [b=blklength, B=blks/line]
p print current code.
q exit.
ssubstitute ch2 for ch1.
S [-] -[gvbB] {keys} Perform the substitution specified by the key.
T [-]|key Transpose text by perm or keyword. e.g. T 4,5,2,3,1
t[/regexp] look for transpositions of period n; [print only /regexp].
B [-]|key apply the specifed rectangular encryption to the text.
b[/regexp] look for block decryptions of size n; [print only
/regexp].
u undo previous modification.
z reset the code to its initial state.
renter code from file.
wwrite code to file.
e edit code.
For information on lots of simple substitution and permutation ciphers see:
Plain: I CAME I SAW I CONQUERED
Cipher: DEREU QNOCI WASIE MACI
Plain: I A E S W C N U R D
C M I A I O Q E E
Cipher: IAESW CNURD CMIAI OQEE
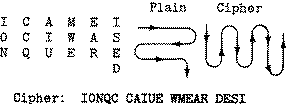
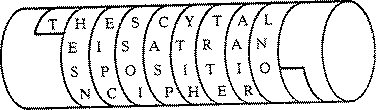
Plain: THESIMPLESTPOSSIBLETRANSPOSITIONSXX
Key (R): 2 5 4 1 3
Key (W): 4 1 5 3 2
T H E S I S T I E H
M P L E S E M S L P
T P O S S S T S O P
I B L E T E I T L B
R A N S P S R P N A
O S I T I T O I I S
O N S X X X O X S N
Cipher: STIEH EMSLP STSOP EITLB SRPNA TOIIS XOXSN
Example - Davies p26 Fig 2.14
Plain: ACONVENIENTWAYTOEXPRESSTHEPERMUTATION
Key (W): C O M P U T E R
Key (W): 1 4 3 5 8 7 2 6
A N O V I N C E
E W T A O T N Y
H E P R T U E M
A O I N Z Z T Z
Cipher: ANOVI NCEEW TAOTN YHEPR TUEMA OINZZ TZ
Example - Davies p26 Fig 2.15
Key(R): sorcery => 6 3 4 1 2 5 7gives
laser beams can be modulated to carry more intelligence than radio waves
erasb lecam snabd umole atoed ctamo ryrre elntl iicee ntgha dnria oesav w
Example - Seberry p67-8 [3]
Seberry Table 3.1 p69
Key(R): s o r c e r y s o r c e r y
Key(R): 6 3 4 1 2 5 7 6 3 4 1 2 5 7
l a s e r b e l a s e r b e
a m s c a n b a m s c a n b
e m o d u l a e m o d u l a
t e d t o c a t e d t o c a
r r y m o r e r r y m o r e
i n t e l l i i n t e l l i
g e n c e t h g e n c e t h
a n r a d i o a n r a d i o
w a v e s w a v e s q r
Example - Sinkov p148
Sinkov p148
Example - Sinkov p 149-151
Plaintext: NOWISTHETIMEFORALLGOODMENExample - Davis Fig2.16 p27
Key (W): L E M O N
2 1 3 5 4
L 2 O N W S I
E 1 H T E I T
M 3 E M F R O
0 5 L A L O G
N 4 D O M N E
Nihilist Cipher: HTEIT ONWSI EMFRO DOMNE LALOG
Diagonal Cipher: ONHET WSEML DAFII TRLOM OOGNE
Substitution Table
\\ A D F G V X
A K Z W R 1 F
D 9 B 6 C L 5
F Q 7 J P G X
G E V Y 3 A N
V 8 O D H 0 2
X U 4 I S T M
Plaintext: PRODUCTCIPHERS
Intermediate Text:
FG AG VD VF XA DG XV
DG XF FG VG GA AG XG
Keyed Block Columnlar Transposition Matrix
D E U T S C H Key
2 3 7 6 5 1 4 Sorted Order
F G A G V D V
F X A D G X V
D G X F F G V
G G A A G X G
Ciphertext: DXGX FFDG GXGG VVVG VGFG CDFA AAXA
This lab we learn about vmware . What is vmware?? Virtual machine software from VMware, that allows multiple copies of the same operating system or several different operating systems to run in the same x86-based machine. For years, VMware has been the leader in virtualization software.
VMware Workstation installation
This is simple step by step on how to install VMware Workstation:
1.Download VMware Workstation from http://www.vmware.com/download/ws/. Then, double click the VMware launcher to start the installation wizards.
2. Click NEXT and choose Typical setup type
3. Choose the location for VMware Workstation installation. Then, click NEXT
4. Configure the shortcuts for the VMware Workstation and click NEXT
5. Click INSTALL. This will take several minutes to finish
6. Enter the serial number for the VMware Workstation.
7. Click FINISH and restart the computer.
0 comments:
Post a Comment